Norman
Allan
| Norman
Allan | |||
Text One: Towards a New natural Philosophy
Chapter
3: Complexification;
dialectic refers
to the complexification of stuff. when things interact they get complex quickly even linear numbers a startling thing about the mandelbrot set 
does it
exist in the world? Pratchett, Stewart and
Cohen ("The Science of Discworld")
"~ SIMPLICITY: During the first two or three hundred moves if the Ant, starting on a completely white grid, it creates tiny patterns which are very simple and often very symmetric. And you sit there thinking 'Of course, we've got a simple rule, so that will give simple patterns, and we ought to be able to describe everything that happens in a simple way.' "~ CHAOS: Then, suddenly, you notice it's not like that any more. You've got a big irregular patch of black and white squares, and the Ant is wandering round in some sort of random walk, and you can't see any structure at all. For Langton's Ant this kind of pseudo-random motion happens for about the next 10,000 steps. So it your computer is not very fast you can sit there for a long time saying 'Nothing interesting is going to happen, it's going to go on like this forever, it's just random.' No, it's obeying the same rule as before. It's just that to us it looks random. "~ EMERGENT ORDER: Finally the Ant locks into a particular kind of repetitive behaviour, and it builds a 'highway'. It goes through a cycle of 104 steps, after which it has moved out two squares diagonally and the shape and colour along the edge are the same as they were at the beginning of that cycle. So that cycle repeats forever, and the Ant just builds a diagonal highway - for ever. "Those
three modes of activity are all consequence of the same rule, but they
are on different levels from the rule itself. There are no rules that talk
about highways. The highway is clearly a simple thing, but a 104-step cycle
isn't a terribly obvious consequence of the rule. In fact the only way mathematicians
can prove that the Ant really does build its highway is to track through
those 10,000 steps. At that point you could say 'Now we understand
why Langton's Ant builds a highway.' But no sooner. "Langton's ant will be our icon for a very important idea: emergence. Simple rules may lead to large, complex patterns. ..." emergence see Langton's Ant All this complexity, Many events in the material world are "linear"
nonlinearity: if
things interact and effect/affect one another... some quotes
from and paraphrasings of Gleick: "Chaos..." Hans Jenny Another
wonderful illustration of complexity Jenny
made a cylindrical "cell" and filled it with a liguid. or a hexagonal pattern..
or aquadralateral pattern...
The
sequence of changes was the same for each cell Jenny
shone a light through the vibrating cell,
Chapter
Four: Neural Net | ||
Chapter 3: Complexification;
dialectic, mandelbrot, and emergence
dialectic refers
to the complexification of stuff.
when it interacts, actions
(and in
particular "interactions")
are implicitly complex -
"three
bodies" is beyond computation.
when things interact they get complex quickly
even linear numbers
when
they act on themselves (recursively)
potentially generate an infinite complexity
(it's as complex as you wish to look, infinitely so).
this is exemplified
in the Julia and Mandelbrot
Sets
(according to Mandelbrot)
the iterative expression z ~> z2
+ C
in the iteration the sum z2 + C replaces
z
and the process is repeated (I think : see footnote)
and when this is graphed out it describes a "Julia set"
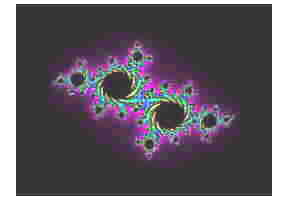
now if the equation z ~> z2 + C goes to infinite
then the Julia set image
it describes
will be made up of separate islands
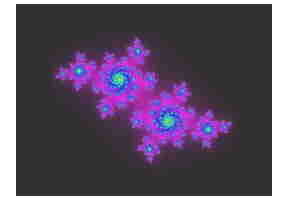
and if the equation is finite then
the set it describes is continuous
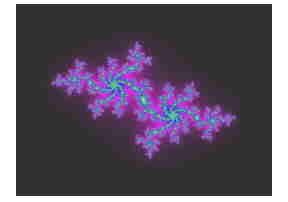
If we map whether the Julia sets go to infinity
or stay finite we get
a graph known as
the mandelbrot set
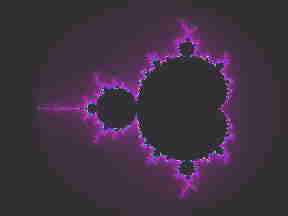
and if we map how quickly or slowly
an equation for the Julia set goes to
infinity
we get the detailed patterns
in the margin of the of the mandelbrot
set
and we can go on expanding bits of this pattern
ad infinitum getting these
intricate pattern
a startling thing about the mandelbrot set
is that as you go deeper and
deeper into it
expanding it in its infinite detail
you will keep returning
to (a little skewed
approximations of) the original "bug"
this example comes from..
.
indeed at any point if you start magnifying it
you will eventually come back
to an approximation
of the original image of the"mandelbrot set"
so some say that the mandelbrot set
is the most complex thing in...
well its not in the universe.
It's an abstraction, a formula.
does it
exist in the world?
Gleick ("Chaos: Making a New Science")
says
when Peitgen and Richter
were modeling the interface between
magnetized
and non-magnetized domains
they found the mandelbrot bug! (footnote
2)
so there may be this infinite complexity
at phase shifts,
for instance, between charged and non-charged space
now note, that this
complexity
is generated in (recursive) linear numeric systems.
(see,
however, footnote 1 where Mandelbrot says the Julia
sets are nonlinear)
Pratchett, Stewart and
Cohen ("The Science of Discworld")
speak of another
aspect of complexity in simple linear systems -
the unpredictable "emergence"
of pattern.
"There is a big gap
between writing down a Theory of Everything and understanding its consequences.
There are mathematical systems that demonstrate this point, and one of the simplest
is Langton's Ant, now the small star of a computer program. The Ant
wanders around on an infinite square grid. Every time it comes to a square,
the square changes colour from black to white or form white to black, and if it
lands on a white square then it turns right, but if it lands on a black square
then it turns left. So we know the Theory of Everything for the Ant's universe
- the rule that governs its complete behaviour by fixing what can happen on the
small scale - and everything that happens in that universe is 'explained' by that
rule.
"When you set the Ant in motion, what you actually
see is three separate modes of behaviour. Everybody - mathematician
or not - immediately spots them. Something in our minds makes us sensitive
to the difference, and it's got nothing to do with the rule. It's the same
rule all the time, but we see three distinct phases:
"~ SIMPLICITY: During the first two or three hundred moves if the Ant, starting on a completely white grid, it creates tiny patterns which are very simple and often very symmetric. And you sit there thinking 'Of course, we've got a simple rule, so that will give simple patterns, and we ought to be able to describe everything that happens in a simple way.'
"~ CHAOS: Then, suddenly, you notice it's not like that any more. You've got a big irregular patch of black and white squares, and the Ant is wandering round in some sort of random walk, and you can't see any structure at all. For Langton's Ant this kind of pseudo-random motion happens for about the next 10,000 steps. So it your computer is not very fast you can sit there for a long time saying 'Nothing interesting is going to happen, it's going to go on like this forever, it's just random.' No, it's obeying the same rule as before. It's just that to us it looks random.
"~ EMERGENT ORDER: Finally the Ant locks into a particular kind of repetitive behaviour, and it builds a 'highway'. It goes through a cycle of 104 steps, after which it has moved out two squares diagonally and the shape and colour along the edge are the same as they were at the beginning of that cycle. So that cycle repeats forever, and the Ant just builds a diagonal highway - for ever.
"Those
three modes of activity are all consequence of the same rule, but they
are on different levels from the rule itself. There are no rules that talk
about highways. The highway is clearly a simple thing, but a 104-step cycle
isn't a terribly obvious consequence of the rule. In fact the only way mathematicians
can prove that the Ant really does build its highway is to track through
those 10,000 steps. At that point you could say 'Now we understand
why Langton's Ant builds a highway.' But no sooner.
"However,
if we ask a slightly more general question, we realize that we don't understand
Langton's Ant at all. Suppose that before the Ant starts we give it an environment
- we paint a few squares black. Now let's ask a simple question: does the
Ant always end up building a highway? Nobody knows. All of
the experiments on computers suggest that it does. On then other hand, nobody
can prove that it does. ... for this very simple mathematical system,
with one simple rule, and a very simple question, where we know the Theory
of Everything - it doesn't tell us the answer.
"Langton's ant will be our icon for a very important idea: emergence. Simple rules may lead to large, complex patterns. ..."
emergence
Simple
rules
may
lead
to
large
complex
patterns
see Langton's Ant
All this complexity,
- the Julia and Mandelbrot
sets, Langton's Ant -
come from simple rules in linear systems.
Many events in the material world are "linear"
- ripples, for example, simply sum -
Brian
Goodwin tells us in "How the Leopard Changed Its Spots"
"From
the study of simpler systems, and particularly from linear approximations ...
a saying had emerged: If you have more than three parameters in your model, anything
is possible!"
however, many
systems act
in a "non-linear" fashion:
they interact, they
effect one another,
and they don't simply sum in a linear manner.
The
behavious of non-linear systems defies computation.
nonlinearity: if
things interact and effect/affect one another...
when we (they, mathematicians)
try to calculate
how this interacting stuff behaves
well you can't
you can't just add it together
it is not linear, if it interacts it doesn't
simply add up
and nonlinear systems defy computation.
and nonlinear systems
can fall into chaos
some quotes
from and paraphrasings of Gleick: "Chaos..."
~ "nonlinear systems generally cannot be solved..." p.23
~ the simplest
of discrete nonlinear systems
exhibits bizarre behaviour
~ simple nonlinear systems do not necessarily
possess simple
dynamical properties
~ mathematically, 'chaos' lurks in dynamic systems
when their nonlinear aspects are not ignored
I personally
first encounter the concept of non-linear oscillation
in the 1960s during
research into the neural organization
of an expressive behaviour -
to
wit, the cherpings of the chick.
which we will encounter
in the next chapter...
Hans Jenny
Another
wonderful illustration of complexity
is found in Hans Jenny's
work with patterns of vibration.
Jenny
made a cylindrical "cell" and filled it with a liguid.
Then he applied a vibration to it. The pattern of vibration,
the waves on the surface, depends on the frequency,
the physical properties
of the liquid (e.g. its viscosity),
and the energy in, the amplitude, of
the vibration.
As the ampliude of the vibration changes,
so does the
pattern of vibration in the cells.
At low amplitudes, as I remember, he saw
concentric waves.
As he increased the amplitude the pattern of waves changed.
Sometimes there would be a bilateral pattern, two waves
going up and down.
At some amplitude it would change to,
say,
a pentagonal pattern....
or a hexagonal pattern..
or aquadralateral pattern...
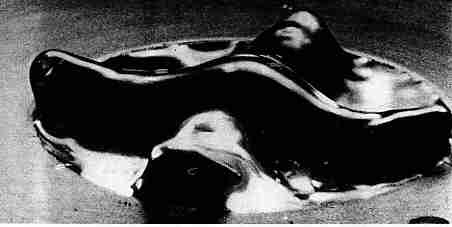
The
sequence of changes was the same for each cell
and particular liquid, but,
with a new set of variables,
it was not predicable!
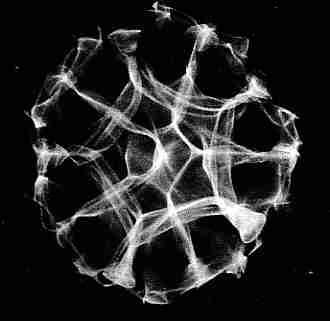
Jenny
shone a light through the vibrating cell,
with
its moving waves, onto a screen
(like sunlight on the bottom of a pool)
and produced these amazing pictures.
Chapter
Four: Neural Net
footnote dialects,
gestalt and synergy
 |